Published
- 4 min read
Binary Tree in Java with unit test
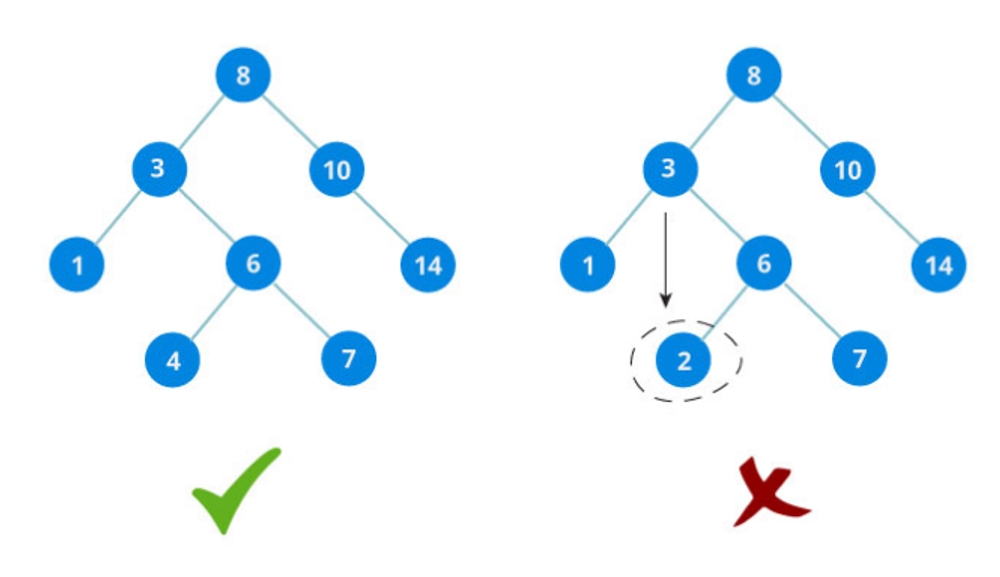
Creating a binary tree in Java, we look at
- Insertion
- Traversal(In Order, Pre Order, Post Order)
- deletion(In Order Predecessor, In Order Successor).
In binary tree recursion is a very important algorithm, it really pushes your understanding. Sometimes i have to go through it with a debugger or some times pen and paper to really understand what is happening, now i think i have a good understanding. Peaks of a debugger.
Anyway a binary tree insert the lesser number of the root to the right and the greater number to the left.
We start with a number 10
10
we add another number 5, 5 is lesser than 10 so it goes to the left.
10
/ \
5
we add another number 20, 20 is greater than 10 so it goes to the right.
10
/ \
5 20
That’s how a binary tree works, each node has at most two children.
Let’s write the INSERTION
We have our class tree, this is what creates each node for us, on creation left and right are null
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int val) {
this.val = val;
left = right = null;
}
}
public class BinaryTree{
TreeNode root;
BinaryTree(){
root = null;
}
public void insert (int val){
root = insertNode(root, val);
}
private TreeNode insertNode(TreeNode root, int val){
if(root == null){
root = new TreeNode(val);
return root;
}
if(val < root.val){
root.left = insertNode(root.left, val);
}else if(val > root.val){
root.right = insertNode(root.right, val);
}
return root;
}
}
When the class is initialised root is set to null, we call insert. if root is null that’s our first value, root is given that value, for another value it check wether it’s greater or lesser than root and assigns it accordingly.
Let’s Look at TRAVERSAL
we have the In order Traversing, it displays the left—>root—>right, the display is between the left and the right.
public void inOrder(){
inOrderTraverse(root);
}
private void inOrderTraverse(TreeNode root){
if(root != null){
inOrderTraverse(root.left);
System.out.print(root.val + "-->");
inOrderTraverse(root.right);
}
}
Then we have the Pre Order Traversal, the display is at the beginning, it displays root—>left—>right
public void preOrder(){
preOrderTraverse(root);
}
private void preOrderTraverse(TreeNode root){
if (root != null) {
System.out.print(root.val + "-->");
preOrderTraverse(root.left);
preOrderTraverse(root.right);
}
}
Last we have the Post Order Traversal, the display is at the end, it displays left—>right—>root
public void postOrder(){
postOrderTraverse(root);
}
private void postOrderTraverse(TreeNode root){
if(root != null){
postOrderTraverse(root.left);
postOrderTraverse(root.right);
System.out.print(root.val + "-->");
}
}
Let’s look at Deletion, When we delete a node that has no child, we don’t need to account for the children so it’s straight forward, when the node has one child when we delete the node, the child of that node becomes the child of the parent node. example
10
/ \
8 20
\
9
If we delete 8 the tree becomes
10
/ \
9 20
When the node to be deleted has two children we have can use two methods for to select who takes it’s place we have the In order successor, it takes the smallest value of the right root. example
15
/ \
10 20
/ \ / \
8 12 17 25
we want to delete 15
In Order Successor will replace the node we want to delete (15) with the smallest number of the number larger than 15 which will be 17, so we start from the right and traverse the left, to find the smallest number.
while In Order Predecessor will replace the node we want to delete(15) with the largest number of the number smaller than 15 which will be 12, so we start from the left and traverse the right, to find the largest number.
public void delete(int key){
root = deleteNode(root, key);
}
private TreeNode deleteNode(TreeNode root, int val){
if(root == null){
return root;
}
if(val < root.val){
root.left = deleteNode(root.left, val);
}else if(val > root.val){
root.right = deleteNode(root.right, val);
}else{
if(root.left == null){
return root.right;
}else if(root.right == null){
return root.left;
}
root.val = predecessor(root.left);
root.left = deleteNode(root.left, root.val);
}
return root;
}
private int predecessor(TreeNode root){
int max_value = root.val;
while(root.right != null){
max_value = root.right.val;
root = root.right;
}
return max_value;
}
In my code here i did an In Order Predecessor, so it check for the largest number from node left.
Then i wrote some unit test to for my functions
package org.example;
import org.junit.jupiter.api.BeforeEach;
import static org.junit.jupiter.api.Assertions.*;
class BinaryTreeTest {
private BinaryTree tree;
@BeforeEach
public void setup(){
tree = new BinaryTree();
}
@org.junit.jupiter.api.Test
void insertNodeToRoot() {
tree.insert(5);
assertNotNull(tree.root);
assertEquals(5, tree.root.val);
}
@org.junit.jupiter.api.Test
void insertMultipleNode(){
tree.insert(5);
tree.insert(4);
tree.insert(10);
assertEquals(4, tree.root.left.val);
assertEquals(10, tree.root.right.val);
}
@org.junit.jupiter.api.Test
void deleteNode(){
tree.insert(5);
tree.insert(6);
tree.insert(10);
tree.delete(6);
assertNull(tree.root.left);
}
@org.junit.jupiter.api.Test
void deleteNodeWithAChild(){
tree.insert(7);
tree.insert(6);
tree.insert(10);
tree.insert(5);
tree.delete(6);
assertEquals(5, tree.root.left.val);
}
@org.junit.jupiter.api.Test
void deleteNodeWithTwoChildren(){
tree.insert(6);
tree.insert(5);
tree.insert(10);
tree.insert(4);
tree.insert(4);
tree.delete(5);
assertEquals(4, tree.root.left.val);
}
}
Checks the root is added, when multiple numbers are added the right and left are of expected values.
Tested for the main functionalities of the binary tree although i didn’t know how to test for the traversals. if you do let me know in the comment.